Funktionen Grundlagen: Verstehe Zuordnungen einfach erklärt | Mathematik

Stell Dir vor, Du gibst Geld in einen Automaten.

Du wirfst 2 Franken ein und erhältst eine Flasche Wasser. Dein Freund wirft ebenfalls 2 Franken ein und bekommt dieselbe Flasche Wasser.

Jeder Betrag führt zu einem eindeutigen Produkt.

Genau so funktionieren mathematische Funktionen: Du gibst eine Zahl hinein und erhältst genau eine Zahl zurück.

Funktionen sind überall: Beim Tanken bestimmt die Literanzahl den Preis. Bei Deinem Handy-Abo bestimmt die Datenmenge die Kosten. In der Physik bestimmt die Zeit die zurückgelegte Strecke. Ohne Funktionen könnten wir keine Vorhersagen treffen und keine Zusammenhänge verstehen.

Jetzt schauen wir uns an, wie die Mathematik dieses alltägliche Prinzip präzise beschreibt.

Eine kleine Zeitreise: Die Geschichte von Funktionen

Die Idee der Funktion ist älter als Du denkst.

Schon die Babylonier vor 4000 Jahren erstellten Tabellen, die Zahlen einander zuordneten. Sie berechneten Quadratzahlen und ihre Wurzeln. Das war bereits eine Form von Funktion, auch wenn sie das Wort nicht kannten.

Die griechischen Mathematiker wie Euklid (ca. 300 v. Chr.) untersuchten geometrische Zusammenhänge. Sie erkannten, dass der Umfang eines Kreises von seinem Radius abhängt. Doch sie formulierten dies nicht als Funktion, sondern als geometrische Beziehung.

Im Mittelalter beschäftigten sich arabische Gelehrte wie Al-Chwarizmi (ca. 780-850 n. Chr.) intensiv mit Gleichungen. Sie entwickelten systematische Methoden, um eine Unbekannte aus einer gegebenen Gleichung zu berechnen. Das war ein wichtiger Schritt zum Funktionsbegriff.

Der Begriff “Funktion” erschien erstmals im 17. Jahrhundert.

Gottfried Wilhelm Leibniz (1646-1716) führte 1673 das Wort “functio” ein. Er meinte damit zunächst geometrische Grössen, die von einem Punkt einer Kurve abhängen. Etwa zur gleichen Zeit entwickelte Isaac Newton (1643-1727) die Infinitesimalrechnung. Beide arbeiteten mit veränderlichen Grössen, die voneinander abhängen.

Im 18. Jahrhundert präzisierte Leonhard Euler (1707-1783) den Funktionsbegriff erheblich. Er schrieb Funktionen als Formeln wie $f(x) = x^2 + 3x$ und führte die heute noch gebräuchliche Notation ein. Euler erkannte, dass eine Funktion eine Vorschrift ist, die jeder Zahl genau eine andere Zahl zuordnet.

Johann Peter Gustav Lejeune Dirichlet (1805-1859) revolutionierte das Verständnis im 19. Jahrhundert. Er definierte eine Funktion als Zuordnung, bei der jedem Element einer Menge genau ein Element einer anderen Menge zugeordnet wird. Diese Definition ist sehr allgemein. Sie verlangt keine Formel mehr. Eine Funktion kann auch durch eine Tabelle oder eine Beschreibung gegeben sein.

Im 20. Jahrhundert wurde der Funktionsbegriff noch abstrakter. Die moderne Mengenlehre betrachtete Funktionen als spezielle Relationen zwischen Mengen. Heute sind Funktionen das zentrale Werkzeug in fast allen Bereichen der Mathematik und Naturwissenschaften. Sie beschreiben Änderungen, Zusammenhänge und Abhängigkeiten.

Die Entwicklung zeigt: Vom praktischen Rechnen mit Tabellen über geometrische Beziehungen bis zur abstrakten Mengenlehre wurde der Funktionsbegriff immer präziser und mächtiger. Heute kannst Du mit Funktionen komplexe Phänomene modellieren: vom Bevölkerungswachstum über Aktienkurse bis zu physikalischen Gesetzen.

Die Grundlagen von Funktionen - Funktionen Grundlagen

Eine Funktion ist eine eindeutige Zuordnung. Jeder Eingabe wird genau eine Ausgabe zugeordnet. Schreibe $f: x \mapsto y$ oder $y = f(x)$. Das bedeutet: Die Funktion $f$ ordnet dem Wert $x$ den Wert $y$ zu.

Definition: Funktion

Eine Funktion $f$ ordnet jedem Element $x$ aus der Definitionsmenge $D$ genau ein Element $y$ aus der Wertemenge $W$ zu. Wir schreiben: $f: D \to W$ oder $y = f(x)$.

Die Definitionsmenge $D$ (auch Definitionsbereich) enthält alle erlaubten Eingabewerte. Nicht jede Zahl ist immer erlaubt. Bei der Funktion $f(x) = \frac{1}{x}$ ist $x = 0$ verboten, weil Division durch null unmöglich ist. Die Definitionsmenge ist hier $D = \mathbb{R} \setminus \{0\}$ (alle reellen Zahlen ausser null).

Die Wertemenge $W$ (auch Wertebereich oder Bildmenge) enthält alle möglichen Ausgabewerte. Bei $f(x) = x^2$ sind alle Ausgabewerte nicht-negativ. Die Wertemenge ist $W = [0, \infty)$.

Das Funktionsargument $x$ ist die Eingabe. Es ist die Variable, die Du in die Funktion einsetzt. Das Funktionsbild $f(x)$ oder $y$ ist die Ausgabe. Es ist der Wert, den die Funktion berechnet.

Ein einfaches Beispiel: $f(x) = 2x + 1$. Diese Funktion verdoppelt die Eingabe und addiert 1. Setze $x = 3$ ein:

$$f(3) = 2 \cdot 3 + 1 = 6 + 1 = 7$$

Die Eingabe 3 wird auf die Ausgabe 7 abgebildet.

Funktionen kannst Du auf verschiedene Arten darstellen. Die analytische Darstellung verwendet eine Formel wie $f(x) = x^2 - 4x + 3$. Die tabellarische Darstellung listet Eingabe-Ausgabe-Paare auf. Die grafische Darstellung zeigt die Funktion als Kurve im Koordinatensystem.

Wichtig ist die Eindeutigkeit: Jeder Eingabe entspricht genau eine Ausgabe. Umgekehrt kann dieselbe Ausgabe zu verschiedenen Eingaben gehören. Bei $f(x) = x^2$ gilt $f(2) = 4$ und $f(-2) = 4$. Beide Eingaben liefern dieselbe Ausgabe.

Das Gegenteil wäre keine Funktion. Würdest Du versuchen, jedem $x$ zwei verschiedene Werte zuzuordnen, hättest Du keine Funktion mehr. Der vertikale Linientest prüft dies grafisch: Schneidet eine senkrechte Linie den Graphen mehr als einmal, ist es keine Funktion.

Funktionen sind das Werkzeug, um Abhängigkeiten zu beschreiben. Du verstehst jetzt, was eine Funktion ist und welche Grundbegriffe wichtig sind.

Die Kernmethode für Funktionen - Funktionen Grundlagen

Um mit Funktionen erfolgreich zu arbeiten, brauchst Du eine systematische Vorgehensweise. Die folgende Methode hilft Dir, Funktionsprobleme sicher zu lösen.

Schritt 1: Identifiziere die Funktion und ihre Bestandteile

Bestimme zunächst die Funktionsgleichung $f(x)$. Finde heraus, welche Variable die Eingabe ist (meist $x$) und wie die Zuordnungsvorschrift lautet. Schreibe die Funktion in der Form $f(x) = \ldots$ oder $y = \ldots$ auf. Achte darauf, dass Du die Vorschrift vollständig verstehst. Bei $f(x) = 3x - 5$ bedeutet dies: Multipliziere $x$ mit 3 und subtrahiere 5.

Schritt 2: Bestimme den Definitionsbereich

Überlege, welche Werte für $x$ erlaubt sind. Prüfe kritische Stellen:

• Bei Brüchen darf der Nenner nicht null sein
• Bei Wurzeln mit geradem Wurzelexponenten muss der Radikand nicht-negativ sein
• Bei Logarithmen muss das Argument positiv sein

Notiere den Definitionsbereich als Menge oder Intervall. Beispiel: $D = \mathbb{R} \setminus \{2\}$ bedeutet alle reellen Zahlen ausser 2.

Schritt 3: Setze Werte ein und berechne Funktionswerte

Ersetze $x$ in der Funktionsgleichung durch den gegebenen Wert. Beachte die Klammerregeln, besonders bei negativen Zahlen. Rechne die arithmetischen Operationen in der richtigen Reihenfolge aus: Potenz vor Punkt vor Strich. Vereinfache das Ergebnis vollständig.

Schritt 4: Bestimme den Wertebereich

Überlege, welche Ausgabewerte möglich sind. Bei einfachen Funktionen erkennst Du dies oft direkt. Quadratfunktionen wie $f(x) = x^2$ liefern nur nicht-negative Werte. Lineare Funktionen wie $f(x) = 2x + 1$ können alle reellen Zahlen annehmen. Notiere den Wertebereich als Menge oder Intervall.

Schritt 5: Kontrolliere Deine Ergebnisse

Setze Deine berechneten Funktionswerte zur Probe wieder in die ursprüngliche Gleichung ein. Prüfe, ob das Ergebnis sinnvoll ist. Negative Wurzeln oder Divisionen durch null deuten auf Fehler hin. Vergleiche mit einer grafischen Darstellung, wenn möglich.

Tipps für jeden Schritt:

• Schreibe alle Zwischenschritte auf
• Verwende Klammern grosszügig, um Fehler zu vermeiden
• Prüfe besonders sorgfältig bei negativen Zahlen
• Achte auf Vorzeichen beim Einsetzen
• Vereinfache schrittweise, nicht alles auf einmal

Definition: Das Grundprinzip von Funktionen - Funktionen Grundlagen

Eine Funktion $f: D \to W$ ordnet jedem Element $x$ aus der Definitionsmenge $D$ genau ein Element $y = f(x)$ aus der Wertemenge $W$ zu. Die Definitionsmenge $D$ enthält alle erlaubten Eingabewerte. Die Wertemenge $W$ enthält alle möglichen Ausgabewerte. Die Eindeutigkeit der Zuordnung ist das zentrale Merkmal einer Funktion.

Beispiel 1: Einstiegsaufgabe

Aufgabe:

Gegeben ist die Funktion $f(x) = 2x + 3$.

• Berechne die Funktionswerte $f(1)$, $f(0)$ und $f(-2)$.
• Gib ausserdem die Definitionsmenge an.

Lösungsweg:

Wir arbeiten Schritt für Schritt durch die Aufgabe.

Schritt 1: Die Funktion analysieren

Die Funktion $f(x) = 2x + 3$ ist eine lineare Funktion. Sie multipliziert die Eingabe ($x$) mit 2 und addiert 3. Die Zuordnungsvorschrift ist klar und einfach.

Schritt 2: Definitionsmenge bestimmen

Bei linearen Funktionen gibt es keine Einschränkungen. Wir dürfen jede reelle Zahl einsetzen. Es gibt keine Division, keine Wurzel, keinen Logarithmus.
Die Definitionsmenge ist:

$$D = \mathbb{R}$$

Schritt 3: Funktionswerte berechnen

Jetzt setzen wir die gegebenen Werte ein.

Für $f(1)$:

$$\begin{align*} f(1) &= 2 \cdot 1 + 3 \\ &= 2 + 3 \\ &= 5 \end{align*}$$

Die Eingabe 1 wird auf die Ausgabe 5 abgebildet.

Für $f(0)$:

$$\begin{align*} f(0) &= 2 \cdot 0 + 3 \\ &= 0 + 3 \\ &= 3 \end{align*}$$

Die Eingabe 0 wird auf die Ausgabe 3 abgebildet.

Für $f(-2)$:

$$\begin{align*} f(-2) &= 2 \cdot (-2) + 3 \\ &= -4 + 3 \\ &= -1 \end{align*}$$

Die Eingabe -2 wird auf die Ausgabe -1 abgebildet.
Achte hier besonders auf das Vorzeichen: $2 \cdot (-2) = -4$.

Schritt 4: Ergebnisse zusammenfassen

Wir haben drei Funktionswerte berechnet:

• $f(1) = 5$
• $f(0) = 3$
• $f(-2) = -1$

Die Definitionsmenge ist $D = \mathbb{R}$.

Beispiel 2: Aufbauende Aufgabe

Aufgabe:

Gegeben ist die Funktion $g(x) = \frac{x + 4}{x - 2}$. Bestimme die Definitionsmenge und berechne $g(0)$ und $g(3)$.

Lösungsweg:

Diese Aufgabe ist anspruchsvoller, weil wir eine Bruchfunktion haben. Der Nenner darf nicht null werden.

Schritt 1: Die Funktion analysieren

Die Funktion $g(x) = \frac{x + 4}{x - 2}$ ist eine gebrochen-rationale Funktion. Der Zähler ist $x + 4$, der Nenner ist $x - 2$.

Schritt 2: Definitionsmenge bestimmen

Der Nenner darf nicht null sein. Wir suchen die Nullstelle des Nenners:

$$\begin{align*} x - 2 &= 0 \\ x &= 2 \end{align*}$$

Bei $x = 2$ ist die Funktion nicht definiert. Die Definitionsmenge ist:

$$D = \mathbb{R} \setminus \{2\}$$

Das bedeutet: Alle reellen Zahlen ausser 2.

Schritt 3: Funktionswerte berechnen

Für $g(0)$:

$$\begin{align*} g(0) &= \frac{0 + 4}{0 - 2} \\ &= \frac{4}{-2} \\ &= -2 \end{align*}$$

Für $g(3)$:

$$\begin{align*} g(3) &= \frac{3 + 4}{3 - 2} \\ &= \frac{7}{1} \\ &= 7 \end{align*}$$

Schritt 4: Unterschied zum ersten Beispiel

Im Gegensatz zum ersten Beispiel müssen wir hier eine Einschränkung beachten. Die Definitionsmenge ist nicht mehr ganz $\mathbb{R}$. Wir können $g(2)$ nicht berechnen, weil 2 nicht im Definitionsbereich liegt.

Ergebnisse:

• Definitionsmenge: $D = \mathbb{R} \setminus \{2\}$
• $g(0) = -2$
• $g(3) = 7$

Beispiel 3: Mittelschwere Aufgabe

Aufgabe:

Gegeben ist die Funktion $h(x) = x^2 - 4x + 3$. Bestimme die Definitionsmenge, berechne $h(-1)$, $h(2)$ und $h(3)$, und gib an, für welche Werte von $x$ die Funktion den Wert 0 annimmt.

Lösungsweg:

Diese Aufgabe kombiniert mehrere Aspekte von Funktionen.

Schritt 1: Definitionsmenge bestimmen

Die Funktion $h(x) = x^2 - 4x + 3$ ist eine quadratische Funktion (Polynom zweiten Grades). Es gibt keine Einschränkungen für $x$. Die Definitionsmenge ist:

$$D = \mathbb{R}$$

Schritt 2: Funktionswerte berechnen

Für $h(-1)$:

$$\begin{align*} h(-1) &= (-1)^2 - 4 \cdot (-1) + 3 \\ &= 1 + 4 + 3 \\ &= 8 \end{align*}$$

Achte auf die Klammern bei $(-1)^2 = 1$ und $-4 \cdot (-1) = 4$.

Für $h(2)$:

$$\begin{align*} h(2) &= 2^2 - 4 \cdot 2 + 3 \\ &= 4 - 8 + 3 \\ &= -1 \end{align*}$$

Für $h(3)$:

$$\begin{align*} h(3) &= 3^2 - 4 \cdot 3 + 3 \\ &= 9 - 12 + 3 \\ &= 0 \end{align*}$$

Schritt 3: Nullstellen bestimmen

Wir suchen Werte von $x$, für die $h(x) = 0$ gilt. Wir haben bereits gesehen, dass $h(3) = 0$. Das ist eine Nullstelle. Wir lösen die Gleichung:

$$\begin{align*} x^2 - 4x + 3 &= 0 \end{align*}$$

Wir können faktorisieren oder die quadratische Lösungsformel verwenden. Faktorisierung:

$$\begin{align*} x^2 - 4x + 3 &= (x - 1)(x - 3) = 0 \end{align*}$$

Die Nullstellen sind $x = 1$ und $x = 3$. Prüfen wir $h(1)$:

$$\begin{align*} h(1) &= 1^2 - 4 \cdot 1 + 3 \\ &= 1 - 4 + 3 \\ &= 0 \end{align*}$$

Tatsächlich ist auch $x = 1$ eine Nullstelle.

Ergebnisse:

• Definitionsmenge: $D = \mathbb{R}$
• $h(-1) = 8$
• $h(2) = -1$
• $h(3) = 0$
• Nullstellen: $x = 1$ und $x = 3$

Die häufigsten Stolpersteine bei Funktionen - Funktionen Grundlagen

Beim Arbeiten mit Funktionen passieren immer wieder dieselben Fehler. Wenn Du diese kennst, kannst Du sie gezielt vermeiden.

⚠️ Achtung: Verwechslung von Funktionswert und Variable

Viele Schüler schreiben $f(x) = 3$ und meinen eigentlich $x = 3$. Das ist ein fundamentaler Unterschied:

• $f(x) = 3$ bedeutet, dass die Ausgabe der Funktion den Wert 3 hat
• $x = 3$ bedeutet, dass die Eingabe den Wert 3 hat

Beispiel: Bei $f(x) = 2x + 1$ ist $f(3) = 7$.

Hier ist $x = 3$ die Eingabe und $f(3) = 7$ die Ausgabe. Wenn Du nach der Eingabe suchst, bei der die Ausgabe 7 ist, löst Du die Gleichung $f(x) = 7$, also $2x + 1 = 7$. Das ergibt $x = 3$.

Merke Dir:

• Die Funktion $f$ ist die Vorschrift
• $x$ ist die Eingabe
• $f(x)$ ist die Ausgabe

Schreibe nie $f = 3$ – das ist mathematisch falsch.

Verwende immer $f(x) = 3$ oder $x = 3$, je nachdem, was Du meinst.

⚠️ Achtung: Fehler beim Einsetzen negativer Zahlen

Beim Einsetzen negativer Zahlen vergessen viele die Klammern. Das führt zu falschen Vorzeichen.

Beispiel: Gegeben ist $g(x) = x^2 - 3x$. Du sollst $g(-2)$ berechnen.

Falscher Ansatz: $g(-2) = -2^2 - 3 \cdot -2 = -4 + 6 = 2$ Hier fehlen die Klammern um $-2$.

Richtig ist: $g(-2) = (-2)^2 - 3 \cdot (-2) = 4 + 6 = 10$

Beachte:

• $-2^2 = -4$ (erst Potenz, dann Vorzeichen)
• $(-2)^2 = 4$ (negative Zahl wird quadriert)

Tipps:

• Setze negative Zahlen immer in Klammern
• Schreibe $-3 \cdot (-2)$ statt $-3 \cdot -2$

Prüfe jeden Term einzeln: $(-2)^2 = 4$, dann $-3 \cdot (-2) = 6$, dann $4 + 6 = 10$.

⚠️ Achtung: Definitionsmenge unvollständig bestimmt

Ein häufiger Fehler ist es, die Definitionsmenge nicht sorgfältig zu prüfen.

Beispiel 1: Bei $h(x) = \dfrac{1}{x^2 - 4}$ denken viele nur an $x \neq 0$. Das ist falsch.

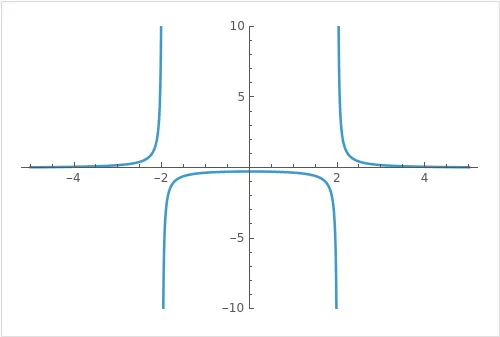
Der Nenner ist $x^2 - 4$. Dieser wird null, wenn $x^2 = 4$, also bei $x = 2$ und $x = -2$.

Korrekte Definitionsmenge: $D = \mathbb{R} \setminus \{-2, 2\}$

Systematisches Vorgehen:

• Setze den Nenner gleich null
• Löse die Gleichung vollständig: $x^2 - 4 = 0 \Rightarrow x^2 = 4 \Rightarrow x = \pm 2$
• Beide Werte müssen ausgeschlossen werden

Merke: Eine quadratische Gleichung hat meist zwei Lösungen.

Beispiel 2: Bei $f(x) = \sqrt{4 - x}$ muss $4 - x \geq 0$ gelten, also $x \leq 4$.

Definitionsmenge: $D = (-\infty, 4]$

⚠️ Achtung: Funktionsgleichung falsch umgeformt

Beim Umformen von Funktionsgleichungen passieren oft Fehler.

Beispiel 1: Du sollst die Gleichung $y = 2x + 3$ nach $x$ auflösen.

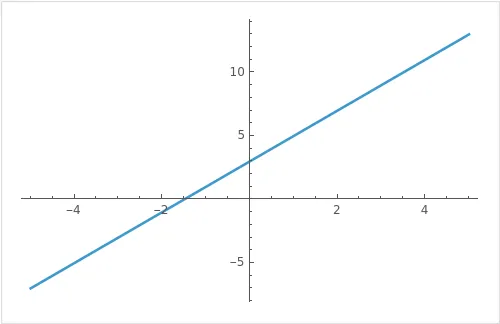
Falscher Ansatz: $x = y - 3 : 2$

Hier wurde die Reihenfolge der Operationen missachtet.

Richtig ist:

• Subtrahiere zuerst 3 von beiden Seiten: $y - 3 = 2x$
• Dann dividiere durch 2: $x = \dfrac{y - 3}{2}$

Die Division gilt für den gesamten Ausdruck $y - 3$, nicht nur für 3.

Beispiel 2: Bei $y = x^2$ folgt nicht einfach $x = \sqrt{y}$.

Die Wurzel hat zwei Lösungen: $x = \pm \sqrt{y}$

Merke:

• Beim Multiplizieren oder Dividieren mit negativen Zahlen dreht sich das Ungleichheitszeichen um
• Arbeite immer schrittweise und prüfe jede Umformung einzeln

Beispiel 4: Komplexere Aufgabe

Aufgabe:

Gegeben ist die Funktion $f(x) = \dfrac{2x - 6}{x^2 - 9}$.

a) Bestimme die Definitionsmenge.

b) Vereinfache die Funktion so weit wie möglich.

c) Berechne $f(0)$ und $f(4)$.

d) Für welchen Wert von $x$ ist $f(x) = 1$?

Lösungsweg:

Diese Aufgabe erfordert mehrere Fähigkeiten: Definitionsbereich bestimmen, Terme faktorisieren und kürzen, Gleichungen lösen.

Teil a: Definitionsmenge bestimmen

Der Nenner darf nicht null sein. Wir lösen:

$$\begin{align*} x^2 - 9 &= 0 \\ x^2 &= 9 \\ x &= \pm 3 \end{align*}$$

Die Werte $x = 3$ und $x = -3$ sind nicht erlaubt. Die Definitionsmenge ist:

$$D = \mathbb{R} \setminus \{-3, 3\}$$

Teil b: Funktion vereinfachen

Wir faktorisieren Zähler und Nenner. Der Zähler ist $2x - 6 = 2(x - 3)$. Der Nenner ist $x^2 - 9 = (x - 3)(x + 3)$ (dritte binomische Formel). Die Funktion wird:

$$\begin{align*} f(x) &= \frac{2(x - 3)}{(x - 3)(x + 3)} \end{align*}$$

Für $x \neq 3$ können wir $(x - 3)$ kürzen:

$$\begin{align*} f(x) &= \frac{2}{x + 3} \quad \text{für } x \neq -3, \, x \neq 3 \end{align*}$$

Wichtig: Die Definitionsmenge ändert sich nicht durch das Kürzen. $x = 3$ bleibt ausgeschlossen, auch wenn $(x - 3)$ gekürzt wurde. Dies ist eine hebbare Definitionslücke.

Teil c: Funktionswerte berechnen

Wir verwenden die vereinfachte Form $f(x) = \frac{2}{x + 3}$.

Für $f(0)$:

$$\begin{align*} f(0) &= \frac{2}{0 + 3} \\ &= \frac{2}{3} \end{align*}$$

Für $f(4)$:

$$\begin{align*} f(4) &= \frac{2}{4 + 3} \\ &= \frac{2}{7} \end{align*}$$

Teil d: Gleichung lösen

Wir suchen $x$ mit $f(x) = 1$. Setze ein:

$$\begin{align*} \frac{2}{x + 3} &= 1 \end{align*}$$

Multipliziere beide Seiten mit $(x + 3)$:

$$\begin{align*} 2 &= x + 3 \end{align*}$$

Subtrahiere 3:

$$\begin{align*} x &= -1 \end{align*}$$

Prüfung: $f(-1) = \frac{2}{-1 + 3} = \frac{2}{2} = 1$. Stimmt.

Der Wert $x = -1$ liegt im Definitionsbereich, also ist die Lösung gültig.

Ergebnisse:

• Definitionsmenge: $D = \mathbb{R} \setminus \{-3, 3\}$
• Vereinfachte Form: $f(x) = \frac{2}{x + 3}$ für $x \neq -3, 3$
• $f(0) = \frac{2}{3}$
• $f(4) = \frac{2}{7}$
• Für $x = -1$ ist $f(x) = 1$

Beispiel 5: Transferaufgabe aus dem Alltag

Aufgabe:

Ein Handy-Abo kostet eine Grundgebühr von 15 Franken pro Monat. Zusätzlich bezahlst Du 20 Rappen pro verbrauchte Minute.

a) Stelle eine Funktion auf, die die monatlichen Kosten $K$ in Abhängigkeit von der Anzahl verbrauchter Minuten $m$ beschreibt.

b) Wie viel kostet das Abo, wenn Du 80 Minuten telefonierst?

c) Du möchtest maximal 35 Franken pro Monat ausgeben. Wie viele Minuten kannst Du höchstens telefonieren?

Lösungsweg:

Diese Aufgabe zeigt, wie Funktionen Alltagssituationen modellieren.

Teil a: Funktion aufstellen

Die monatlichen Kosten setzen sich aus zwei Teilen zusammen: Grundgebühr und verbrauchsabhängige Kosten.

Grundgebühr: 15 Franken (fest).

Kosten pro Minute: 20 Rappen = 0.20 Franken.

Bei $m$ Minuten betragen die verbrauchsabhängigen Kosten $0.20 \cdot m$ Franken.

Die Gesamtkosten sind:

$$K(m) = 15 + 0.20 \cdot m$$

Die Definitionsmenge ist $D = [0, \infty)$, da Du nicht negativ viele Minuten telefonieren kannst.

Teil b: Kosten für 80 Minuten berechnen

Setze $m = 80$ in die Funktion ein:

$$\begin{align*} K(80) &= 15 + 0.20 \cdot 80 \\ &= 15 + 16 \\ &= 31 \end{align*}$$

Das Abo kostet 31 Franken, wenn Du 80 Minuten telefonierst.

Teil c: Maximale Minutenanzahl bestimmen

Du möchtest maximal 35 Franken ausgeben. Wir lösen die Gleichung $K(m) = 35$:

$$\begin{align*} 15 + 0.20 \cdot m &= 35 \end{align*}$$

Subtrahiere 15 von beiden Seiten:

$$\begin{align*} 0.20 \cdot m &= 20 \end{align*}$$

Dividiere durch 0.20:

$$\begin{align*} m &= \frac{20}{0.20} \\ &= 100 \end{align*}$$

Du kannst maximal 100 Minuten telefonieren, um bei 35 Franken zu bleiben.

Prüfung: $K(100) = 15 + 0.20 \cdot 100 = 15 + 20 = 35$. Stimmt.

Interpretation:

Diese Funktion ist linear mit Steigung 0.20 und y-Achsenabschnitt 15. Die Steigung gibt die Kosten pro zusätzlicher Minute an. Der y-Achsenabschnitt ist die Grundgebühr. Solche Funktionen begegnen Dir oft bei Tarifen, Mietkosten oder Liefergebühren.

Ergebnisse:

• Funktion: $K(m) = 15 + 0.20m$ mit $D = [0, \infty)$
• Kosten für 80 Minuten: 31 Franken
• Maximale Minutenanzahl für 35 Franken: 100 Minuten

Übungs-Sektion im Arbeitsblatt-Stil

Aufgabe 1: Gegeben ist die Funktion $f(x) = 3x - 7$. Berechne die Funktionswerte $f(2)$, $f(0)$ und $f(-3)$.

Aufgabe 2: Bestimme die Definitionsmenge der Funktion $g(x) = \frac{5}{x + 4}$.

Aufgabe 3: Die Funktion $h(x) = 2x + 5$ ordnet jedem Wert $x$ einen Wert $h(x)$ zu. Welcher Wert von $x$ ergibt den Funktionswert $h(x) = 13$?

Aufgabe 4: Gegeben ist die Funktion $k(x) = x^2 + 2x - 8$. Berechne $k(-3)$ und $k(4)$. Bestimme ausserdem die Nullstellen der Funktion.

Aufgabe 5: Ein Taxifahrer verlangt eine Grundgebühr von 5 Franken plus 3 Franken pro gefahrenem Kilometer. Stelle eine Funktion $T(k)$ auf, die den Preis in Abhängigkeit von den gefahrenen Kilometern $k$ beschreibt. Wie viel kostet eine Fahrt über 12 Kilometer?

Aufgabe 6: Bestimme die Definitionsmenge und vereinfache die Funktion $m(x) = \frac{3x - 12}{x^2 - 16}$ so weit wie möglich.

Aufgabe 7: Gegeben ist die Funktion $p(x) = \frac{2}{x - 3} + 1$. Bestimme die Definitionsmenge und berechne $p(5)$. Für welchen Wert von $x$ ist $p(x) = 0$?

Aufgabe 8: Ein rechteckiges Grundstück hat eine feste Breite von 20 Metern. Die Länge $l$ kann variieren. Stelle eine Funktion $A(l)$ auf, die die Fläche des Grundstücks in Abhängigkeit von der Länge beschreibt. Wie lang muss das Grundstück sein, damit die Fläche 300 Quadratmeter beträgt? Wie lang darf es maximal sein, wenn die Fläche 500 Quadratmeter nicht überschreiten soll?

Aufgabe 9: Untersuche die Funktion $q(x) = \frac{x^2 - 1}{x + 1}$. Bestimme die Definitionsmenge, vereinfache die Funktion und berechne die Nullstellen. Was passiert an der Stelle $x = -1$?

Aufgabe 10: Eine chemische Reaktion verläuft nach der Funktion $C(t) = 100 - 4t^2$, wobei $C$ die Konzentration eines Stoffes in Gramm pro Liter und $t$ die Zeit in Minuten ist. Bestimme die sinnvolle Definitionsmenge (bedenke: Die Konzentration kann nicht negativ werden). Nach welcher Zeit ist die Konzentration auf 36 g/L gesunken? Wann ist der Stoff vollständig verbraucht?

Das Wichtigste in Kürze

Eine Funktion ist eine eindeutige Zuordnung, bei der jedem Element der Definitionsmenge genau ein Element der Wertemenge zugeordnet wird. Diese Eindeutigkeit ist das zentrale Merkmal. Du schreibst $f: x \mapsto y$ oder $y = f(x)$. Jedem $x$ entspricht genau ein $y$, aber verschiedene $x$-Werte können dasselbe $y$ ergeben.

Die Definitionsmenge $D$ enthält alle erlaubten Eingabewerte. Prüfe kritische Stellen sorgfältig: Bei Bruchfunktionen darf der Nenner nicht null sein. Bei Wurzelfunktionen mit geradem Wurzelexponenten muss der Radikand nicht-negativ sein. Bei Logarithmusfunktionen muss das Argument positiv sein. Schreibe die Definitionsmenge als Menge oder Intervall auf.

Die Wertemenge $W$ enthält alle möglichen Ausgabewerte. Sie hängt von der Art der Funktion ab. Lineare Funktionen können meist alle reellen Zahlen annehmen. Quadratfunktionen wie $f(x) = x^2$ ergeben nur nicht-negative Werte. Die Wertemenge erkennst Du oft durch Analyse der Funktion oder durch grafische Darstellung.

Beim Einsetzen von Werten beachte die Klammerregeln besonders bei negativen Zahlen. $(-2)^2 = 4$, aber $-2^2 = -4$. Setze negative Zahlen immer in Klammern, um Vorzeichenfehler zu vermeiden. Rechne alle Zwischenschritte aus und vereinfache schrittweise.

Funktionen beschreiben Abhängigkeiten im Alltag. Preis-Mengen-Beziehungen, Zeit-Weg-Funktionen oder Kosten-Nutzen-Analysen sind praktische Anwendungen. Die Fähigkeit, reale Situationen durch Funktionen zu modellieren, ist eine wichtige mathematische Kompetenz. Du übersetzt die Situation in eine mathematische Sprache.

Die historische Entwicklung zeigt die wachsende Präzision des Funktionsbegriffs. Von babylonischen Tabellen über Eulers Formelschreibweise bis zu Dirichlets abstrakter Mengendefinition wurde der Begriff immer allgemeiner. Heute sind Funktionen das grundlegende Werkzeug in allen quantitativen Wissenschaften.

Quiz: Teste dein Wissen

Frage 1: Was ist der fundamentale Unterschied zwischen f(x) = 3 und x = 3?

Die Gleichung $f(x) = 3$ bedeutet, dass die Ausgabe der Funktion den Wert 3 hat. Die Gleichung $x = 3$ bedeutet, dass die Eingabe den Wert 3 hat. Das sind zwei völlig verschiedene Aussagen.

Bei $f(x) = 3$ fragst Du: Bei welchen Eingabewerten liefert die Funktion die Ausgabe 3? Das ist eine Gleichung, die Du nach $x$ auflösen musst.

Bei $x = 3$ ist die Eingabe festgelegt. Du könntest nun den Funktionswert $f(3)$ berechnen.

Beispiel: Gegeben $f(x) = 2x - 1$. Die Frage “Für welches $x$ ist $f(x) = 3$?” führt zu $2x - 1 = 3$, also $x = 2$. Die Frage “Was ist $f(3)$?” führt zu $f(3) = 2 \cdot 3 - 1 = 5$.

Merke: $f$ ist die Vorschrift, $x$ ist die Eingabe, $f(x)$ ist die Ausgabe. Verwechsle diese drei Begriffe nie.

Frage 2: Warum muss bei der Funktion g(x) = 1/(x² - 9) nicht nur x = 3, sondern auch x = -3 aus der Definitionsmenge ausgeschlossen werden?

Der Nenner $x^2 - 9$ wird null, wenn $x^2 = 9$ gilt. Diese Gleichung hat zwei Lösungen: $x = 3$ und $x = -3$. Beide Werte machen den Nenner null, was verboten ist.

Viele denken nur an $x = 3$, weil das die positive Lösung ist. Das ist ein häufiger Fehler. Quadratische Gleichungen haben meist zwei Lösungen.

Du kannst es auch durch Einsetzen prüfen: $3^2 - 9 = 9 - 9 = 0$ und $(-3)^2 - 9 = 9 - 9 = 0$. Beide Werte führen zur Division durch null.

Die korrekte Definitionsmenge ist deshalb $D = \mathbb{R} \setminus \{-3, 3\}$. Vergiss nie, alle Lösungen der Nenner-Nullstellen-Gleichung zu finden.

Frage 3: Eine Funktion ist durch die Wertepaare (1,4), (2,7), (3,10), (4,13) gegeben. Welche Funktionsgleichung könnte dahinterstecken?

Schaue Dir die Wertepaare an und suche ein Muster. Die Ausgabewerte sind 4, 7, 10, 13. Der Unterschied zwischen aufeinanderfolgenden Werten ist immer 3. Das deutet auf eine lineare Funktion mit Steigung 3 hin.

Eine lineare Funktion hat die Form $f(x) = mx + c$. Die Steigung $m = 3$ haben wir erkannt. Jetzt bestimmen wir $c$ durch Einsetzen eines Wertepaares.

Wähle $(1, 4)$: $4 = 3 \cdot 1 + c$, also $c = 1$.

Die Funktionsgleichung ist $f(x) = 3x + 1$.

Prüfung: $f(1) = 4$, $f(2) = 7$, $f(3) = 10$, $f(4) = 13$. Alle Wertepaare stimmen. Diese Methode funktioniert, wenn die Funktion linear ist. Bei anderen Funktionstypen brauchst Du andere Ansätze.

Frage 4: Warum ist die Wertemenge der Funktion f(x) = x² + 1 nicht ganz ℝ, sondern nur [1, ∞)?

Die Funktion $f(x) = x^2 + 1$ setzt sich aus zwei Teilen zusammen: $x^2$ und der Addition von 1.

Der Term $x^2$ ist immer nicht-negativ. Egal welchen Wert $x$ annimmt, $x^2 \geq 0$. Der kleinste Wert von $x^2$ ist 0, erreicht bei $x = 0$.

Wenn Du 1 addierst, ist der kleinste mögliche Funktionswert $f(0) = 0^2 + 1 = 1$. Die Funktion kann nie kleiner als 1 werden.

Für grosse Beträge von $x$ wird $x^2$ beliebig gross, also auch $f(x)$. Die Funktion kann jeden Wert grösser oder gleich 1 annehmen.

Deshalb ist die Wertemenge $W = [1, \infty)$. Das Intervall beginnt bei 1 (inklusive) und geht bis unendlich. Werte kleiner als 1 sind nicht erreichbar. Diese Analyse zeigt, wie wichtig das Verständnis der Funktionsstruktur ist.

Ausblick: Der nächste Schritt auf deiner Mathe-Reise

Jetzt kennst Du die Grundlagen von Funktionen. Der nächste logische Schritt ist die Untersuchung spezieller Funktionstypen. Du wirst lineare Funktionen detailliert analysieren: Steigung und y-Achsenabschnitt bestimmen, Graphen zeichnen, Nullstellen berechnen. Danach folgen quadratische Funktionen mit ihren charakteristischen Parabeln. Du lernst die Scheitelpunktform kennen und verstehst, wie Streckungen und Verschiebungen funktionieren. Später kommen Exponential- und Logarithmusfunktionen hinzu, die Wachstumsprozesse beschreiben. Alle diese speziellen Funktionen bauen auf dem Fundament auf, das Du jetzt gelegt hast. Die Begriffe Definitionsmenge, Wertemenge und Funktionswert begleiten Dich durch die gesamte Funktionenlehre. Ohne dieses Grundverständnis wären die komplexeren Themen nicht zugänglich.

Lösungen zur Übungs-Sektion

Lösung 1:

Wir setzen die gegebenen Werte in die Funktion $f(x) = 3x - 7$ ein.

Für $f(2)$:

$$\begin{align*} f(2) &= 3 \cdot 2 - 7 \\ &= 6 - 7 \\ &= -1 \end{align*}$$

Für $f(0)$:

$$\begin{align*} f(0) &= 3 \cdot 0 - 7 \\ &= 0 - 7 \\ &= -7 \end{align*}$$

Für $f(-3)$:

$$\begin{align*} f(-3) &= 3 \cdot (-3) - 7 \\ &= -9 - 7 \\ &= -16 \end{align*}$$

Ergebnis: $f(2) = -1$, $f(0) = -7$, $f(-3) = -16$

Lösung 2:

Die Funktion $g(x) = \frac{5}{x + 4}$ ist eine Bruchfunktion. Der Nenner darf nicht null sein.

$$\begin{align*} x + 4 &\neq 0 \\ x &\neq -4 \end{align*}$$

Ergebnis: Die Definitionsmenge ist $D = \mathbb{R} \setminus \{-4\}$.

Lösung 3:

Wir suchen $x$ mit $h(x) = 13$. Setze in die Funktionsgleichung ein:

$$\begin{align*} 2x + 5 &= 13 \end{align*}$$

Subtrahiere 5 von beiden Seiten:

$$\begin{align*} 2x &= 8 \end{align*}$$

Dividiere durch 2:

$$\begin{align*} x &= 4 \end{align*}$$

Prüfung: $h(4) = 2 \cdot 4 + 5 = 8 + 5 = 13$. Stimmt.

Ergebnis: $x = 4$

Lösung 4:

Wir berechnen zunächst die Funktionswerte.

Für $k(-3)$:

$$\begin{align*} k(-3) &= (-3)^2 + 2 \cdot (-3) - 8 \\ &= 9 - 6 - 8 \\ &= -5 \end{align*}$$

Für $k(4)$:

$$\begin{align*} k(4) &= 4^2 + 2 \cdot 4 - 8 \\ &= 16 + 8 - 8 \\ &= 16 \end{align*}$$

Nullstellen: Wir lösen $k(x) = 0$:

$$\begin{align*} x^2 + 2x - 8 &= 0 \end{align*}$$

Faktorisierung oder quadratische Lösungsformel. Wir faktorisieren:

$$\begin{align*} (x + 4)(x - 2) &= 0 \end{align*}$$

Die Nullstellen sind $x = -4$ und $x = 2$.

Ergebnis: $k(-3) = -5$, $k(4) = 16$, Nullstellen: $x = -4$ und $x = 2$

Lösung 5:

Die Funktion setzt sich aus Grundgebühr und kilometerabhängigen Kosten zusammen:

$$T(k) = 5 + 3k$$

Für 12 Kilometer:

$$\begin{align*} T(12) &= 5 + 3 \cdot 12 \\ &= 5 + 36 \\ &= 41 \end{align*}$$

Ergebnis: $T(k) = 5 + 3k$, eine Fahrt über 12 Kilometer kostet 41 Franken.

Lösung 6:

Zunächst bestimmen wir die Definitionsmenge. Der Nenner darf nicht null sein:

$$\begin{align*} x^2 - 16 &= 0 \\ x^2 &= 16 \\ x &= \pm 4 \end{align*}$$

Die Definitionsmenge ist $D = \mathbb{R} \setminus \{-4, 4\}$.

Jetzt vereinfachen wir. Faktorisiere Zähler und Nenner:

$$\begin{align*} m(x) &= \frac{3(x - 4)}{(x - 4)(x + 4)} \end{align*}$$

Für $x \neq 4$ kürzen wir $(x - 4)$:

$$\begin{align*} m(x) &= \frac{3}{x + 4} \quad \text{für } x \neq -4, \, x \neq 4 \end{align*}$$

Ergebnis: $D = \mathbb{R} \setminus \{-4, 4\}$, vereinfachte Form: $m(x) = \frac{3}{x + 4}$

Lösung 7:

Die Funktion ist $p(x) = \frac{2}{x - 3} + 1$. Der Nenner darf nicht null sein:

$$\begin{align*} x - 3 &\neq 0 \\ x &\neq 3 \end{align*}$$

Die Definitionsmenge ist $D = \mathbb{R} \setminus \{3\}$.

Für $p(5)$:

$$\begin{align*} p(5) &= \frac{2}{5 - 3} + 1 \\ &= \frac{2}{2} + 1 \\ &= 1 + 1 \\ &= 2 \end{align*}$$

Für $p(x) = 0$:

$$\begin{align*} \frac{2}{x - 3} + 1 &= 0 \\ \frac{2}{x - 3} &= -1 \end{align*}$$

Multipliziere mit $(x - 3)$:

$$\begin{align*} 2 &= -(x - 3) \\ 2 &= -x + 3 \\ x &= 1 \end{align*}$$

Prüfung: $p(1) = \frac{2}{1 - 3} + 1 = \frac{2}{-2} + 1 = -1 + 1 = 0$. Stimmt.

Ergebnis: $D = \mathbb{R} \setminus \{3\}$, $p(5) = 2$, $p(x) = 0$ für $x = 1$

Lösung 8:

Die Fläche eines Rechtecks ist Länge mal Breite:

$$A(l) = 20 \cdot l = 20l$$

Für $A = 300$ Quadratmeter:

$$\begin{align*} 20l &= 300 \\ l &= 15 \end{align*}$$

Für $A \leq 500$ Quadratmeter:

$$\begin{align*} 20l &\leq 500 \\ l &\leq 25 \end{align*}$$

Ergebnis: $A(l) = 20l$, für 300 m² muss $l = 15$ m sein, für maximal 500 m² darf $l \leq 25$ m sein.

Lösung 9:

Definitionsmenge: Der Nenner darf nicht null sein:

$$\begin{align*} x + 1 &\neq 0 \\ x &\neq -1 \end{align*}$$

Die Definitionsmenge ist $D = \mathbb{R} \setminus \{-1\}$.

Vereinfachung: Faktorisiere den Zähler mit der dritten binomischen Formel:

$$\begin{align*} q(x) &= \frac{(x - 1)(x + 1)}{x + 1} \end{align*}$$

Für $x \neq -1$ kürzen wir $(x + 1)$:

$$\begin{align*} q(x) &= x - 1 \quad \text{für } x \neq -1 \end{align*}$$

Nullstellen der vereinfachten Form:

$$\begin{align*} x - 1 &= 0 \\ x &= 1 \end{align*}$$

Bei $x = -1$ hat die ursprüngliche Funktion eine hebbare Definitionslücke. Der gekürzte Term $x - 1$ würde bei $x = -1$ den Wert $-2$ ergeben, aber die Funktion ist dort nicht definiert.

Ergebnis: $D = \mathbb{R} \setminus \{-1\}$, vereinfacht: $q(x) = x - 1$, Nullstelle: $x = 1$, bei $x = -1$ ist eine hebbare Definitionslücke.

Lösung 10:

Die Konzentration kann nicht negativ werden. Wir lösen $C(t) \geq 0$:

$$\begin{align*} 100 - 4t^2 &\geq 0 \\ 100 &\geq 4t^2 \\ 25 &\geq t^2 \\ t^2 &\leq 25 \end{align*}$$

Dies gilt für $-5 \leq t \leq 5$. Da die Zeit nicht negativ sein kann, ist die sinnvolle Definitionsmenge $D = [0, 5]$.

Für $C(t) = 36$:

$$\begin{align*} 100 - 4t^2 &= 36 \\ 64 &= 4t^2 \\ 16 &= t^2 \\ t &= \pm 4 \end{align*}$$

Da $t \geq 0$, ist $t = 4$ Minuten die Lösung.

Vollständig verbraucht ist der Stoff, wenn $C(t) = 0$:

$$\begin{align*} 100 - 4t^2 &= 0 \\ 100 &= 4t^2 \\ 25 &= t^2 \\ t &= 5 \end{align*}$$

Ergebnis: Sinnvolle Definitionsmenge: $D = [0, 5]$, nach 4 Minuten ist die Konzentration 36 g/L, nach 5 Minuten ist der Stoff vollständig verbraucht.